Lean 初见笔记

目录
  1. 假装这是前言
  2. Preparation
    1. Install
    2. The book
    3. Basics
    4. Tactic

Lean 4 是一个功能强大的交互式定理证明器和编程语言，结合了逻辑推理与编程，主要用于形式化验证、数学证明以及高可靠性软件开发。Lean 4 提供了一个灵活的类型系统和高性能的编译器，使其在理论研究和实际应用中都有出色表现。 —— GPT 说的。

F*ck 我为什么要去看这种东西啊（悲） —— 我说的

假装这是前言

\senioria/

这篇博客我会尝试用英语写。

Preparation

Install

Follow the guide at https://leanprover-community.github.io/get_started.html

The book

I’m firstly reading Mathematics in Lean to start. It is the standard mathematics-oriented reference is Mathematics in Lean, recommended by Lean Community. Unlike other popular languages, you may need a high perspective of math to learn Lean.

  • Senioria: linca这种动态语言迷居然觉得lean爽 x（超小声（
  • Me: no 我是在用它作为定理证明 （看上去就好坐牢

（……真的有人会用Lean这种语言去写代码吗……学术代码例外）

Unlike other languages, in general, if you just open a single .lean file in your text editor and try to compile it, you’ll get a bunch of confusing errors.

Thus, you should strictly follow the guide, if you’re a starter. I suggest this because I messed up my environment just by swapping a step (oh…), that’s my personal experience.

如果你是初学者，你应该严格的遵守安装指南。这是我的亲身体会，你只需要交换一个看上去微不足道的步骤就能搞坏你的环境。（毕竟初学者）

Every non-trivial piece of Lean code needs to live inside a Lean project (sometimes also called a Lean package). A “Lean project” is more than just a folder that you’ve named “My Lean stuff”. Rather, it’s a folder containing some very specific things: in particular, a git repository and a file lakefile.lean that gathers information about dependencies of the project, including for instance the version of Lean that should be used.

Basics

Learn requires us to justify each step in a calculation. For example:

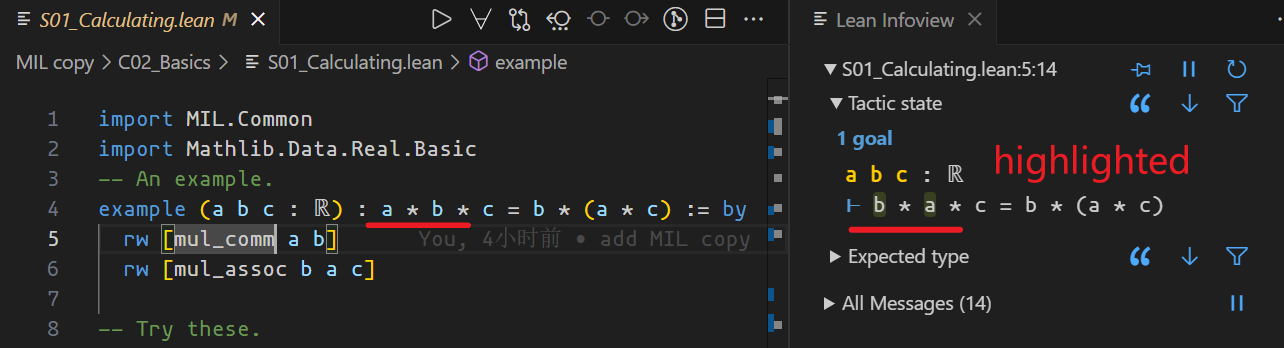
example (a b c : ℝ) : a * b * c = b * (a * c) := by
  rw [mul_comm a b]
  rw [mul_assoc b a c]

The rw means “rewrite”. And the mul_comm here means Commutative property of multiplication（乘法交换律）. So, rw [mul_comm a b] means “rewrite patterns match (a * b) to (b * a)”.

You can see the replaced formula in VSCode here:

mul_comm_20240903184037.png

And \l (←) stands for right-to-left equation replacement. For example:

example (a b c : ℝ) : b * (a * c) = a * b * c := by
  rw [← mul_assoc b a c]
  rw [← mul_comm a b]

It is the reverse of the previous proof.

Tactic

It will be annoying to write duplicated basic formulas, for example if we are proving this:

example : g + a + d + e + b + h + f + c = a + b + c + d + e + f + g + h := by
  rw [add_comm g]
  rw [add_assoc a, add_comm g, ← add_assoc]
  rw [add_assoc (a + d), add_comm g, ← add_assoc]
  rw [add_assoc (a + d + e), add_comm g, ← add_assoc]
  rw [add_assoc (a + d + e + b), add_assoc (a)]
  rw [add_assoc a, add_comm (d + e), ← add_assoc a]
  rw [add_assoc (a + b + (d + e)), add_comm (g + h)]
  rw [add_assoc (a + b + (d + e)), add_comm (f + (g + h)), ← add_assoc]
  rw [add_assoc (a + b), add_comm (d + e)]
  rw [← add_assoc, ← add_assoc, ← add_assoc, ← add_assoc]

We reordered the items tediously, but this is something that a human would know is correct at first glance. In fact, Lean requires a rigorous proof, so this is essential, but we can let the computer do this boring work for us. We need to introduce a magic: Tactic

The ring tactic is imported indirectly when we import Mathlib.Data.Real.Basic, but we will see in the next section that it can be used for calculations on structures other than the real numbers. It can be imported explicitly with the command import Mathlib.Tactic. We will see there are similar tactics for other common kind of algebraic structures.

The ring tactic is designed to prove identities in any commutative ring as long as they follow purely from the ring axioms, without using any local assumption. So we can rewrite the tedious proof above, with only one line:

example : g + a + d + e + b + h + f + c = a + b + c + d + e + f + g + h := by
  ring

到这里 2.1. Calculating 的内容就结束了，今天就先写到这里。

2024-09-03CodeMathPrograming LanguageLean