PFPL 笔记 - VI Dynamic Types · Zero Calorie Drink Shop

笔记 6
最详细的一集，因为我要讲解这部分（摊手
但是读得很开心！这章真是让我受益匪浅啊！

Chapter 17 The Untyped Lambda Calculus ¶

许多实际使用的编程语言宣称自己是无类型的（untyped），然而这只是一种假象。这些语言实际上是单一类型的(uni-typed)而非无类型。

Lambda 演算，丘奇于 1930 年提出。它唯一的“特性”就是高阶函数（higher-order function），即：

一切都是函数，
每个表达式都可以被应用于一个参数，而该参数本身也必须是一个函数，
最终的结果仍然是一个函数。

Statics ¶

The statics of $\mathcal L\{\lambda\}$ is defined by general hypothetical judgments of the form

x1 ok, x2 ok, ..., xn ok |- u ok

stating that u is a well-formed expression involving the variables x1 ~ xn

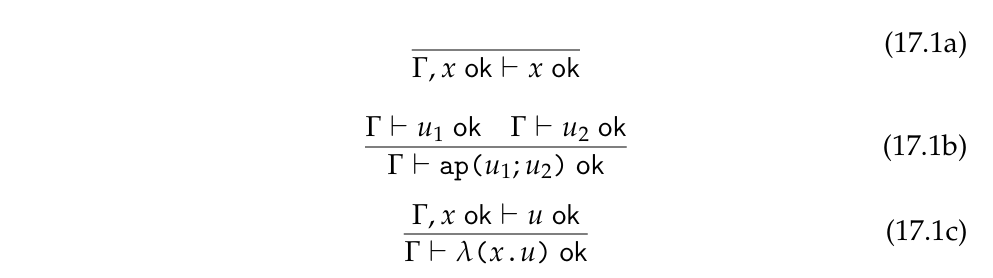
若 x 在环境 Γ 中已声明为合法，则 x 本身是合法的。
若 u₁ 和 u₂ 都是合法表达式，则它们的应用 ap(u₁; u₂) 也是合法的。
若在环境 Γ 下 x ok 则 u ok 则 λ(x . u) 也是合法的。

Dynamics ¶

λ-演算的 dynamics 不是通过传统的 transition system 来定义，而是通过 equaitonally（至少 PFPL 里这样定义）

Definitional equality for $L$ is a judgment of the form $\Gamma \vdash u, u'$ , where $\Gamma \vdash$ x1 ok,...,xn ok for some n 0, and u and u’ are terms having at most the variables x1 … xn free. It is inductively defined by the following rules

自反性

$\dfrac{}{\Gamma, u \text{ ok} \vdash u \equiv u}$
对称性

$\dfrac{\Gamma, u \text{ ok} \vdash u \equiv u'}{\Gamma, u \text{ ok} \vdash u' \equiv u}$

传递性

$\dfrac {\Gamma, u \text{ ok} \vdash u \equiv u' \quad \Gamma, u \text{ ok} \vdash u' \equiv u''} {\Gamma, u \text{ ok} \vdash u \equiv u''}$

……

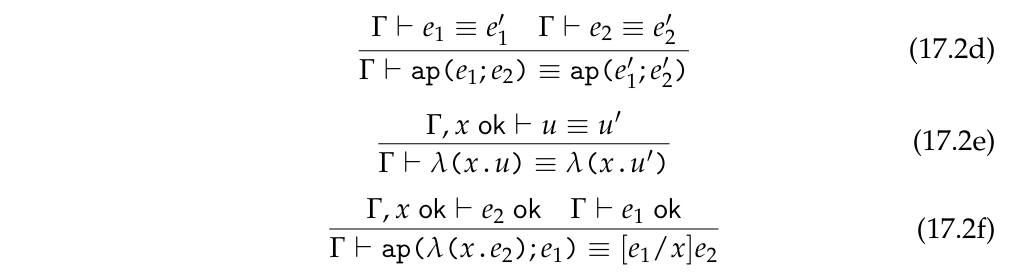
We often write just $u \equiv u'$ when the variables involved need not be emphasized or are clear from context.

Definablity ¶

无类型 λ-演算的一个重要特性是它的表达能力。它是一个图灵完备（Turing-complete） 的语言，也就是说，它和任何已知的编程语言一样，都可以表达自然数上的所有可计算函数。

Chuch’s Law: 任何可计算的函数都有其 Lambda Calculus 等价表达

作为例子，我们证明 lambda 演算至少和 PCF 一样强：

我们可以用 lambda 的形式定义自然数，which 叫丘奇数

Church Numerals ¶

为了懒得打 latex 下面用 \a -> b 表示 $\lambda(a)b$

    0 = \b -> \s -> b
n + 1 = \b -> \s -> s(n(b)(s))

表示原文的

注意到，b 可以解释为 blank，或者说初始值，而 s 可以解释为 successor

也就是说这里定义了 0 是用 blank 和 successor 两个组合子构造出的一个 lambda，

这样，运用 successor 到 n(b)(s) i.e. 用 b，s 实例化了的 n 就能得到 n + 1

另外一个有趣的事情是，当我们得到 n 这个丘奇数（它自己也是一个函数）的时候，显然 n f g 是 g(g(g(... n个g...(f))))，也就是说这个数字就能用来作为 n-fold

比如展开后

1 = \b -> \s -> s(b)
2 = \b -> \s -> s(s(b))
3 = \b -> \s -> s(s(s(b)))
...

那么自然数运算也就很好理解了

举例

succ = \x -> \b -> \s -> s(x(b)(s))

故

succ 0  = \b -> \s -> s( 0(b)(s) )
        = \b -> \s -> s(b)
        = 1

plus = \x -> \y -> y(x)(succ)

可以理解为
plus x y 就是将 x 作为初始值，调用 y (x) succ 当然就是 “x + y”

例如，展开 plus 1 2

= 1(2)(succ)
= (\b -> \s -> s(b))(2)(succ)
= succ(s(2))
= 3

对于乘法

times = \x -> \y -> y(0)(plus(x))

则是将原先的 successor 换成了 plus(x) 后的新 y，显然这就是 y * x

times 2 2
= 2(0)(plus 2)
= (\s -> s(s(0)))(plus 2)
= plus 2 (plus 2) 0
= 4

一些简单验算

ghci> b = 0
ghci> s x = x+1
ghci> zero = \b -> \s -> b
ghci> succ = \x -> \b -> \s -> s(x(b)(s))
ghci> ghci> succ zero b s
1
ghci> plus = \x -> \y -> y(x)(succ)
ghci> one = succ zero
ghci> one b s
1
ghci> plus one one b s
2
ghci> two = succ one
ghci> plus one two b s
3

要定义 ifz(u; u0; x.u1) 需要一些技巧，因为我们需要找到一个前驱函数 pred

pred 0 = 0
pred (n + 1) = n

这并不是听起来那么容易因为相当于我们需要能把一大坨的高阶函数里的 s(n) 的 n 拿出来，而且还需要考虑 0 的存在

可以借鉴移位的思想，如果有 $(n-1, n) \to (n, n+1)$ 的推导就能很容易拿到 n - 1

Church Pairs ¶

先定义丘奇风格的 pair

(括号好多懒得打……不如把 f(a)(b) 写成 f a b 好了)

pair u1 u2 = \f -> f u1 u2

left  u = u(\x -> \y -> x)
right u = u(\x -> \y -> y)

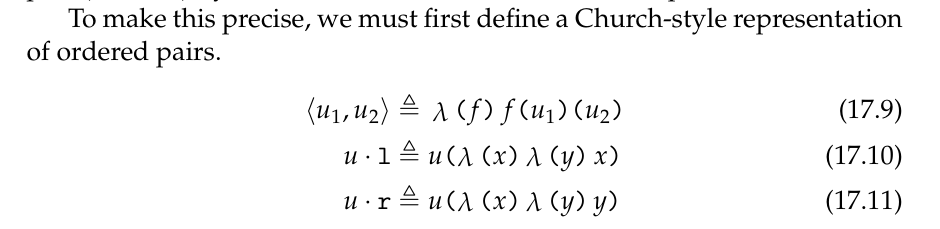
然后，注意到我们之前定义的 Church Numeric 的 b 和 s 都是可以替换成任意的实例的！因此，只需要把 <0, 0> 作为 b 传入，就能获得一个带有 predecessor 的 Church numberic.

pred' = \x -> x ([0, 0])(\y -> [right y, succ(right y)])
pred  = \x -> right (pred' x)

这样我们就获取了需要的 pred 函数。这样，ifz 也很好定义了

ifz u, u0, x, u1 = u(u0)(\never -> [(pred u)/x] u1)

现在我们还差 general recursion。一如既往地，lambda calculus 的函数是没有名字的，我们需要得到一个 fix 让 general recursion 存在

Y 组合子 ¶

最出名的 fix point combinator 是 Y 组合子

Y = \F -> (\f -> F(f(f))) (\f -> F(f(f)))

验算

Y(F)
= (\f -> F(f(f)))(\f -> F(f(f)))
= F((f)(f)) where f = \f -> F(f f)
= F(
  (\f -> F(f(f)))(\f -> F(f(f)))
  )
= F(Y(F))

看到这里我非常的震撼，人们是如何构造出这样神奇的组合子的？原书接下来做了解释：

让我们抛开内存和地址空间这些不谈。假如有一个函数

function fib(x) {
  return x > 1 ? fib(x - 1) + fib(x - 2) : 1;
}

现在我们忘记函数可以有名字。为了还能实现递归，自然而然的，我们会尝试加一个参数，self 或者 this 之类的，这样这个函数就知道了自己是什么。

function tmp(self, x) {
  return x > 1 ? self(self, x - 1) + self(self, x - 2) : 1;
}
function fib(x) {
  reutnr tmp(tmp, x);
}

注意到 tmp(tmp, ...args) 的存在！为了更好看出来，我们把它写成柯里化的 lambda 函数

const tmp = (self) => (x) => {
  return x > 1 ? self(self)(x - 1) + self(self)(x - 2) : 1;
};
const fib_1 = (x) => {
  return tmp(tmp)(x);
};
// 然后 x 可以消掉
const fib = tmp(tmp);
// fib

因此，对于任何一个我们需要递归的函数 F = \self -> 函数体, 构造

F' = \f -> F(f(f))

能帮我们把每次 F 里的 self 换成 self(self)

此时观察到

F'(F') == F(F'(F'))

F'(F') 就是我们想要的 F 的不动点。现在把它展开，就得到了

(\f -> F(f(f)))(\f -> F(f(f)))

于是我们就得到了 Y 组合子，可以得到任意 F 的 fixed point

Scott’s Theorem ¶

Scott 定理表明：

在无类型 λ-演算中，定义相等性是不可判定的，即不存在算法可以确定两个 λ-项是否相等。

inseparability

$\mathcal A_0$ 和 $\mathcal A_1$ 是 insparability (不可区分的)，当且仅当没有一个决定性的属性 $\mathcal B$ such that

$\mathcal A_0 \ u$ implies $\mathcal B \ u$
$\mathcal A_1 \ u$ implies not the case that $\mathcal B \ u$

behavioral

$\mathcal A$ 是 behavioral (行为属性)，当且仅当 $u \equiv u'$ 则 $\mathcal A$ iff $\mathcal u'$

Scott 定理有两部分：

任何两个非平凡的属性 A 和 B 是不可区分的

（如果某个属性对所有 untyped terms 都成立，或者对任何 untyped terms 都不成立，则该属性被称为平凡的。）

也就是说这里引入了一个构造 v 是 w(x) 的反面，同时根据 lemma 17.1 它又得能接受一个自身到自身，所以矛盾了

这里放点我自己的思考不知道对不对 ¶

我们应该也能用图灵机的停机问题的思想去证明 Scott 定理。（虽然维基百科说 Scott’s Theorem 比停机问题还早 XD）

在 1936 年邱奇利用 λ 演算给出了对于判定性问题（Entscheidungsproblem）的否定：关于两个 lambda 表达式是否等价的命题，无法由一个“通用的算法”判断，这是不可判定性能够证明的头一个问题，甚至还在停机问题之先。 ——维基百科

首先，Lambda 演算的停机问题也是不可判定的，可以直接照搬图灵机的证明

定义 λ-演算的停机：给定一个 λ-项 M 如果经过有限步 β-归约后到达一个正常形式（normal-form），即不再能进行 β-约简，则称 M 停机。

如果存在 lambda 演算 Halt 可以判定一个 lambda 演算 F 在参数 args 的时候是否停机，比如

Halt(F)(args) = 0 当F停机
Halt(F)(args) = 1 当F不停机

则我们可以构造一个 U
U = \P -> ifz(Halt(P)(P); Y(Y); 0)

则考虑 Halt(U)(U)，
若 Halt(U)(U) = 0，则 U(U) 应当跑一个无限递归，矛盾
若 Halt(U)(U) = 1，则 U(U) 应当直接返回0，不停机，矛盾

所以不存在一个lambda演算 Halt 可以判定任意 lambda 演算 F 在参数 args 的时候是否停机。

利用停机问题不可判定性，

如果 lambda 演算 Equiv 能判定两个 lambda 演算是否相同 （相同返回0，不同返回1）
则构造

A = \f -> \args -> 0
B = \f -> \args -> ifz(f(args); 0; 0)

（我们假定 f(args) 应该在停机的时候得到一个 church numeral）

那么A 和 B 相同当且仅当 f(args) 停机。Equiv 规约到停机问题，故不存在。

还有一些有趣的补充 ¶

无类型的 λ 演算系统被证明在用于逻辑系统的时候是不自洽的——在 1935 年斯蒂芬·科尔·克莱尼和 J. B. Rosser 举出了 Kleene-Rosser 悖论

考虑 $P = \lambda (f) \neg f(f)$ 则 $P(P) = \neg P(P)$ 所以我们可以找到一个等于其否定的项。

这提醒我们，有必要清楚地区分哪些 lambda 项可以代表命题，哪些 lambda 不能，这导致了项的类型概念。

Untyped MeansUni-Typed ¶

无类型的 λ 演算可以被忠实地嵌入到具有递归类型的类型语言中。这意味着每个无类型 λ 项都可以表示为一个带类型的表达式，使得表示的执行对应于项自身的执行。

这种嵌入并不是通过在 L 中编写一个解释器（这当然是可以实现的），而是通过直接将无类型 λ 项表示为具有递归类型的带类型表达式。

关键观察是：无类型的 λ 演算实际上是单类型的 λ 演算。赋予其强大功能的并非类型缺失，而是它只有一个类型，即递归类型

D = μt.t → t

D 类型的值形式为 fold(e)，其中 e 是 D→D 类型的值——一个其定义域和值域均为 D 的函数。-任何这样的函数都可以“卷起”被视为 D 类型的值，而任何 D 类型的值都可以“展开”转换为函数。递归类型通常可以被视为类型同构方程的解，此处的方程是 D = D → D。这表明 D 是一个与其自身上的函数空间同构的类型，这在传统的集合论中是不可能的，但在基于计算的 λ 演算环境中是可行的。

由此可见，所谓的无类型语言 L{ lambda } 尽管在术语上与类型语言相对立，实际上仍然是一种带类型的语言。无类型语言并非消除了类型，而是将无限集合的类型合并为一个递归类型。这使得静态类型检查变得 trivial，但代价是在值与递归类型之间进行强制转换时带来了显著的动态开销。

在第 18 章中，我们将更进一步，允许许多不同类型的值（而不仅仅是函数），每种类型都是“主”递归类型的组成部分。这表明所谓的动态类型语言实际上是静态类型语言。因此，这一传统区别几乎不能被视为对立，因为动态语言不过是静态语言的一种特殊形式，强调了一个递归类型。

Chapter 18 Dynamic Typing ¶

17 章介绍了 untyped lambda calculus，其中所有 term 都同构于一个函数。因此，不会因为值的误用而发生运行时错误，因为所有参数都是函数。

但一旦语言中允许不止一类值，这个特性就会失效。例如，如果我们将自然数作为 primitive 添加到无类型演算中（而不是通过 Church 编码定义它们），那么尝试将数字应用于参数或将函数添加到数字时可能会引发运行时错误。

语言设计中的一种思想流派是将这种缺点转化为优点，即采用一种具有单一类型 (type), 多个值类 (value class) 的计算模型。这种语言被称为动态类型语言，与静态类型语言相对立。但这种所谓的对立是虚幻的：正如所谓的 untyped 演算实际上是 uni-typed 类型的一样，动态语言最终也只是静态语言的受限形式。这句话非常重要，值得重复：每种动态语言本质上都是静态语言，我们将自己限制在（不必要的）受限类型规则中以确保安全。

Dynamically Typed PCF ¶

Dynamically typed version of $\mathcal L \{\text{nat} \rightharpoonup \}$ called $\mathcal L \{dyn\}$

现在我们有两种 value： numbers 和 functions。succ 和 zero 不是值，在这里是一种算符，来产生 value.

递归虽然可以用 fixed point combinator 定义，但是我们这里把它定义成原型类型 (primitive) 来简化 chapter 18.3 中的分析。

对于这些动态语言来说，具体语法往往具有欺骗性，因为它掩盖了抽象语法的一个重要细节：即每个值都标有一个在运行时发挥重要作用的分类器(classifier)（我们很快就会看到）。

因此，尽管数字 n 的具体语法只是单纯地 $\overline n$ ，但抽象语法表明该数字被标记为类别(class) num，以表明该值属于数字类别。这样做是为了将其与函数值区分开来，函数值具体具有形式 $\lambda (x) d$ ，但其抽象语法 fun 表示要用标签 fun 对其进行分类，以将其与数字区分开来。

注：这里你可以认为 tag 是变量类别 class（而非类型，type）的 id

这种标记在任何动态语言中都是至关重要的，因此，在下文中密切关注抽象形式非常重要。

Statics ¶

显然。而之前一样，只需要检验一下 expression 里面有没有自由变量就行。

$x_1 \text{ ok}, ..., x_n \text{ ok} \vdash d \text{ ok}$

Dynamics ¶

作为动态语言的 $\mathcal L \{dyn\}$ 需要检查之前 $\mathcal L \{\text{nat} \rightharpoonup \}$ 永远不可能发生的一些错误。比如，函数调用的时候需要判断一下那个被调用的是不是真的是一个函数。

注意后四条判断只有在 d val 的时候有意义。这些 affirmative class checking judgments 第二个参数代表的是 value 的底层结构，它本身不是 value。

Lemma 18.1 (Class Checking) 如果 d val 则

either d is_num for some n or d isnt_num;
either d is_fun x.d’ for some x and d’, or d isnt_fun

证明显然。

Theorem 18.2 (Progress): If d ok then either d val or d err, or there exists d’ such that $d \mapsto d'$

Theorem 18.3 (Exclusivity): 对此语言中的任意 d ，下面恰有一个成立：d val, d err, $d \mapsto d'$ for some d’

Variations and Extensions ¶

在之前的 $\mathcal L \{\text{nat} \rightharpoonup \}$ 中我们使用 zero 和 succ 来定义 nat。在 $\mathcal L \{dyn\}$ 中，我们直接定义了 numberals。这样做是为了确保只有一个数字类，而不是 zero 和 succ 两个单独的 class。

另一种方法是将 zero 和 succ(d) 视为两个单独 class 的值，并为它们分别引入 class checking 判断。这会使错误检查规则复杂化，并允许出现有问题的值，例如 succ(lambda (x)d)，但它允许我们避免使用 class of numbers。当以这种风格书写时，条件分支的 dynamics 如下所示：

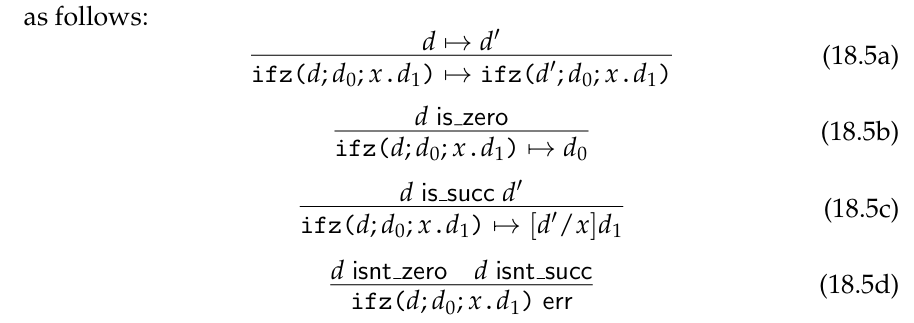
注意 successor class 的前驱不一定要是一个 number，虽然我们前面的公式不可能产生这种可能性。

接下来结构化数据也是容易加入的。

注意上面这个函数，显然，你可以直接把任何值用在这两个函数上，无论它们是不是列表。如果 arg1 不是列表，会产生错误并终止，但是该函数不会遍历参数 arg2，所以 arg2 是任何值都可以。

有人会觉得，用 null 来分辨 pair 不是合适的，因为这语言包含不止这两种 classes。一种可能的手段是，完全放弃 pattern matching 想法，直接用 general 的 conditional branch 去分辨 null

此处引入一个小插曲：为什么叫 cons 和 car 和 cdr 呢？~~小编也很好奇~~

这是来自 lisp 的习惯，在 1950s Lisp 最早被实现的时候，car 和 cdr 分别是两个寄存器：

car (“contents of the address part of register number”) “寄存器号地址部分的内容”

cdr (“contents of the decrement part of register number”), “寄存器号递减部分的内容”

而 cons 直接是 constructor 的缩写，指的是 list 的构造子

现在 append 可以用下面的公式给出：

fix a is \x -> \y -> cond(x; cons(car(x); a(cdr(x))(y)); y)

看不太清的话就是

append x y = case cond x of
  anyhow -> cons (car x) (append (cdr x) y)
  nil -> y

这种 append 公式的行为与之前的公式没有什么不同；唯一的区别是，我们不再根据值是否为 nil 或 pair 来进行分派，而是根据值的谓词来进行区分，其中包括特殊情况的检查。

还有另一种方式，即增强而非限制条件分支，让它包含语言中所有可能的值类别，比如在具有 num, fun, null, pair 的的语言中，条件将会有四个分支。这种方法的困难是，现实语言中会有许多数据类型，这样会非常笨重。

此外，即使我们已经对值的类别进行了指派，与该类别的原始操作也需要进行运行时检查，例如，我们可以确定值 d 属于数字类，但没有办法将此信息传播到条件分支中。加法运算仍然必须检查 d 的类别，获取底层数字，并创建一个新的数字类值。这是动态语言的固有限制，它不允许处理除分类值之外的其他值

Critique of Dynamic Typing - 对动态类型的批判 ¶

像 $\mathcal L \{dyn\}$ 这样的语言的 safety theorem 经常被宣传为动态类型相比于静态类型的优势。与排除了某些类型错误的静态语言不同， $\mathcal L \{dyn\}$ 中的每一段抽象语法基本上都是格式良好的，因此，根据定理 18.2，具有定义良好的动态性。

但这也可以看作是一个缺点，因为在 $\mathcal L \{dyn\}$ 中，本该通过类型检查在编译时排除的错误直到运行时才会显现。并且为了实现这一点， $\mathcal L \{dyn\}$ 的 dynamic 必须强制执行静态类型语言中不需要检查的条件。

考虑加法

\x -> fix p is \y -> ifz y { zero => x | succ(y') => succ(p(y'))}

注意到，fix pointer 把 p 绑定到了该函数，这意味着在递归调用中，ap(p) 的动态检查总是会成功，但是 $\mathcal L \{dyn\}$ 没有办法取消这种冗余检查，因为它没有能力表达 that “p 始终的将绑定到一个不变的 function”。

其次，内部的 lambda-abstraction 的 apply 要么是 x，要么是 x 的递归的 successor。也就是说除了基本情况外后面的情况都可以保证通过 class check，但我们没有能力表达这一点，successor 只能每次都老老实实地进行 class check

Classification 不是免费的——tag 需要存储空间，每次使用时都需要花时间将类与值分离，每次创建类时又需要花时间将类附加到值上。虽然分类的开销不是渐近显著的（它只会使程序变慢一个常数），但它仍然是不可忽略的，应该尽可能消除。但这在 $\mathcal L \{dyn\}$ 中是不可能的，因为它无法表达所需不变量所需的限制。

为此，我们需要一个静态类型系统。

Chapter 19 Hybrid Typing ¶

混合语言是一种将静态类型和动态类型相结合的语言，它通过为静态类型语言添加一个独特的动态值类型 dyn 来丰富它。

第 18 章中讨论的动态类型语言可以通过将动态类型程序视为 dyn 类型的静态类型程序来嵌入到混合语言中。这表明静态类型和动态类型并不相互对立，而是可以和谐共存。

然而，混合语言的概念本身就是虚幻的，因为 dyn 类型实际上是一种特殊的递归类型。不需要任何特殊的机制来支持动态类型。相反，它们可以从更一般的递归类型概念中派生出来。此外，这表明动态类型只是静态类型的一种使用方式。因此，动态类型和静态类型之间的所谓对立是一种谬论。动态类型只是静态类型的一种特殊情况。

A Hybrid Language ¶

这里的 new 当然和 C++ 里的不一样，这里的 new 是添加一个 classifier 到 value，而 cast 是检查这个 classifier，然后返回对应的 value。

几个定理：

有 sum type 和 recursive type 的语言里 dyn 不需要是一个 primitive。

Dynamic as Static Typing ¶

$\mathcal L \{dyn\}$ 可以嵌入到 $\mathcal L \{\text{nat dyn } \rightharpoonup\}$ 中，只需要一个简单的翻译

Optimization of Dynamic Typing ¶

考虑之前提到的那个加法函数。

我们之前已经指出它具有大量可以在静态类型版本中消除的开销。消除这些开销需要静态类型

由于动态语言只能表示一种类型的值，因此不可能在动态语言中表达优化后的形式。动态语言所声称的自由——即由于省略了类型而带来的灵活性——实际上对语言的表达能力施加了严重的限制，相比之下，具有动态值类型的静态语言则更具表现力。

首先，关于前文所说 p 绑定递归的低效性。我们只需要简单地把 p 的类型改成 dyn -> dyn 就能直接表达 p 是一个作用于动态值函数的不变量。

fun ! λ (x : dyn) fun ! fix p : dyn -> dyn is λ (y : dyn) e'(x,p,y')

其中 e'(x,p,y') 是

ifz (y ? num) { zero ⇒ x | succ(y') ⇒ num ! (s(p(num! y') ? num)) }.

这样，循环内部的 p 就无须 tag check 了。

接下来，观察到类型为 dyn 的参数 y 在每次循环迭代时都会被转换为一个数字，然后才会被测试是否为零。由于此函数是递归的，参数 y 在两种情况下会绑定到值：

在最初调用加法函数时。
在每次递归调用时。

但是，递归调用是在 y 的 predecessor 上进行的，而前驱一定是一个自然数。在调用点上，它被标记为 num，但在下一次迭代的条件检查中却会被移除。这表明，我们应该在循环外部就对 y 进行类型转换，避免在递归调用中对参数进行类型转换。

这样做会改变函数的类型，从 dyn -> dyn 变为 nat -> dyn。因此，还需要进一步更改，以确保整个函数保持类型正确。

继续观察。递归调用的结果会进行检查，以确保其类别是 num，然后对底层值进行递增，并将其标记为 num。如果递归调用的结果来自条件语句的这个分支，则显然类别检查是多余的，因为我们已经知道它必须具有 num 类别。但如果结果来自条件语句的另一个分支呢？在这种情况下，函数返回 x，但 x 不一定是 num，因为它是由函数的调用者提供的。然而，我们可以合理地认为，向加法函数传递非数值参数是一个错误。这可以通过将条件分支中的 x 替换为 x ? num 来强制执行。

结合这些优化，我们得到内循环 e''(x) 的最终形式如下：

fix p : nat -> nat is λ (y : nat) ifz y { zero ⇒ x ? num | succ(y') ⇒ s(p(y')) }.

这个函数的类型是 nat -> nat，并且在应用于自然数时会以全速运行——所有的检查都已经从内部循环中移除。

最后，回顾一下我们的整体目标：我们希望定义一个加法函数，该函数作用于 dyn 类型的值。因此，我们需要一个 dyn -> dyn 的值，而当前我们得到的是 nat -> nat。可以通过在前面预加一个 num 类型转换，并在后面加一个 num 类型的强制转换来获得所需的形式：

fun ! λ (x : dyn) fun ! λ (y : dyn) num ! (e''(x) (y ? num)).

最内层的 λ-抽象通过组合类检查将 e’'(x) 从 nat -> nat 转换为 dyn -> dyn，确保 y 在初始调用时是一个自然数，并将结果重新标记为 dyn。

这些转换的结果是，计算的内部循环可以“全速”运行，不需要对函数或数字进行 tag check。而加法函数的最外层仍然保持为 dyn 类型的值，它封装了一个柯里化函数，接收两个 dyn 类型的参数。这种方式保留了所有对加法函数的调用的正确性，即传递和返回 dyn 类型的值，同时优化其执行过程。

当然，我们还可以去除加法函数的类标签，将其类型从 dyn 更改为更具描述性的 dyn -> dyn -> dyn。但这要求调用者不能将加法视为 dyn 类型的值，而必须将其视为一个函数，该函数必须依次应用于两个 dyn 类型的值，并且它们的 class 必须是 num。如果程序员可以控制在哪里调用该函数，就可以进行这样的转换，并不会有什么问题。只有在可能存在程序员无法直接控制的外部 call 时，才有必要将加法函数封装为 dyn 类型的值。

从这个原则出发，我们可以得出一个更广泛的结论：动态类型的作用仅限于系统的“边缘”，即那些涉及不受控制的调用的地方。在系统的内部，仅使用 dyn 类型没有任何好处，反而会带来相当大的弊端。

Static Versus Dynamic Typing ¶

动态类型的支持者曾试图通过各种方式区分动态语言和静态语言。我们可以从当前的视角来重新审视这些所谓的区别。

“动态语言将类型与值关联，而静态语言将类型与变量关联。”
但这种说法是错误的，源于将“类型”（types）与“类别”（classes）混淆的错误认识。动态语言实际上是通过标记（tagging）来将 class 与 value 关联，比如使用 num 和 fun 这样的标识符。这种分类方法本质上等同于在静态类型语言中使用递归和 sum types。因此，这并不是动态语言的一个独特特性。此外，静态语言不仅为变量分配类型，还为表达式分配类型。由于动态语言本质上是一种特殊的静态语言（仅包含单一类型），因此它们同样也为表达式分配类型。

举一点现实语言的例子。比如 C 标准库的 qsort 为
```
void qsort(
    void* ptr, size_t count, size_t size,
    int (*comp)(const void*, const void*)
);
```
其实这里的 void* 就充当了某种 dyn 的作用。C++ 中也有更现代的 std::any
```
#include <any>
#include <iostream>
int main() {
  std::any a = 1;
  std::cout << a.type().name() << ": " << std::any_cast<int>(a) << '\n';
  a = 3.14;
  std::cout << a.type().name() << ": " << std::any_cast<double>(a) << '\n';
  a = true;
  std::cout << a.type().name() << ": " << std::any_cast<bool>(a) << '\n';

  // Outputs:
  // double: 3.14
  // bool: true
  // bad any_cast
}
```
“动态语言在运行时检查类型，而静态语言在编译时检查类型。”
这也是一个错误的说法。动态语言和静态语言在本质上都是静态类型的，只不过动态语言采用了一种退化的类型系统，即只有一个类型。如我们所见，动态语言确实会在运行时进行类别检查（class checks），但静态语言中如果允许 sum types，同样也需要执行类别检查。真正的区别仅在于类别检查的使用范围：在动态语言中，类别检查是始终必须的；而在静态语言中，类别检查只在必要时才会进行。
“动态语言支持异构集合，而静态语言只支持同构集合。”

（这句话说的是，你可以在动态语言中构造 [1, true, "foo", { bar: null }] 这样元素类型不同的集合，而这些人认为静态语言中做不到这一点）

这同样是一个错误的说法。静态语言中的 sum types 本来就是用于支持异构数据的，任何支持 sum type 的静态语言都可以表示异构数据结构。例如，考虑以下列表：
```
cons(num(1); cons(fun(λ(x)x); nil))
```
有人认为在静态语言中无法表示这样的列表，因为它的元素类型不同。然而，无论是在静态语言还是动态语言中，这种列表实际上都是类型同构（type homogeneous）的，只不过它的元素类别可能是异构（class heterogeneous）的。在上述列表中，所有元素的类型都是 dyn，但第一个元素的类别是 num，第二个元素的类别是 fun。

在这里我们甚至也能给出一个现实生活的例子： Crystal 语言。一个编译的、native 的静态语言。它支持以类型 itself 为 tag 的 sum type（或者被叫作 union type），所以你很容易写出
```
arr = [] of (Int32 | String)
arr.push(1)
arr.push("qwq")
puts arr # 输出 [1, "qwq"]
```
这很好的打破了这句话。

所以，我们该如何看待动态语言和静态语言之间的这种所谓的区别呢？

与其说它们是对立的，不如说动态语言实际上是静态语言的一种使用方式。每一种动态语言本质上都是一种静态语言，只不过它的类型系统极为有限（只有一个类型！）。然而，正如我们之前所看到的，类型对于程序的正确性和效率至关重要，它们不仅用于表达程序的不变性（invariants），还用于强制执行这些不变性。因此，动态语言的“自由”实际上是一种受限的自由，牺牲了类型信息所能提供的优势。